Teorema de Bayes: Entenda o que é e como calcular

Quando pretendemos saber a probabilidade de um evento acontecer tendo como base um evento inicial, precisamos aplicar o Teorema de Bayes.
Dessa forma, o teorema de Bayes é uma fórmula famosa de estatística, sendo muito usado por investidores na bolsa de valores.
O que é o teorema de Bayes?
O teorema de Bayes é uma fórmula de probabilidade que calcula a possibilidade de um evento acontecer, com base em um conhecimento que pode estar relacionado ao evento.
O Bayes Theorem foi desenvolvido por Pierre-Simon Laplace que publicou a fórmula em 1812 no seu livro Teoria Analítica de Probabilidade.
No entanto, ele recebe este nome por conta do pastor e matemático inglês Thomas Bayes ter sido a primeira pessoa a fornecer uma equação permitindo que novas evidências atualizassem a probabilidade de um evento a partir de um conhecimento a priori.
A grande questão do teorema de Bayes é que é necessário ter alguma informação anterior, ou seja, saber que um determinado evento já ocorreu, e qual é a probabilidade dele.
Alguns investidores utilizam essa fórmula para estimar probabilidades no mercado financeiro. Essa fórmula pode ser utilizada para relacionar índices com ações individuais, como, por exemplo a chance da Petrobrás (PETR4) cair após uma queda do índice Bovespa.
Qual a fórmula do teorema de Bayes?
Para calcular um evento (A), considerando que um evento (B) ocorreu, é preciso usar a seguinte fórmula matemática:
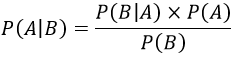
Onde:
- P(A|B): Probabilidade do evento A acontecer;
- P(B|A): Probabilidade de B acontecer, dado que A já ocorreu;
- P(A): Probabilidade de A ocorrer;
- P(B): Probabilidade de B acontecer.
Portanto, ao aplicar essa fórmula é possível saber qual é a probabilidade da união de dois eventos, considerando eventos mutuamente exclusivos.
Exemplos com o Teorema de Bayes
Para facilitar o entendimento, pode-se utilizar exemplo com uma caixa que contenha duas bolas vermelhas e três bolas azuis.
Nesse exemplo, considere que duas bolas são retiradas ao acaso, uma na sequência da outra sem que a primeira tenha sido recolocada.
Qual a probabilidade da segunda bola (evento B) ser vermelha, considerando que a primeira (evento A) seja azul?
Qual a probabilidade da primeira bola (evento A) ser azul, considerando que a segunda bola retirada (evento B), será vermelha?
Para responder a primeira questão é preciso usar a fórmula da probabilidade condicional. Uma vez com o resultado encontrado, aplica-se a fórmula do Teorema de Bayes para achar a resposta para a segunda questão.

]
Regra de Bayes no problema de Monty Hall
O paradoxo de Monty Hall é um dos problemas mais controversos que refletem uma mudança de probabilidade baseada em um grau de crença.
Esse problema também é conhecido como jogo das portas, e para entendê-lo, nada melhor do que exemplificá-lo.
Vamos imaginar que você está participando de um programa de TV e precisa escolher uma entre três portas. Uma delas contém um prêmio, as outras duas não.
Assim que você escolhe uma porta, a sua probabilidade de acerto é de ⅓. Porém, logo depois da sua escolha o apresentador abre uma porta vazia, e pergunta se você quer trocar de porta.
Aí vem a questão: se você trocar de porta, as suas chances de ganhar o prêmio aumentam? A resposta para essa questão é sim.
Se você continuar na porta escolhida as suas chances de ganhar continuam sendo de ⅓, já se você trocar de porta elas aumentam para ⅔. Vamos entender o porquê.
Entendendo o problema de Monty Hall
Para entender o problema de Monty Hall, vamos primeiro definir os eventos do exemplo que demos acima:
- A = Porta escolhida (nº 1) tem o prêmio
- B = Porta vazia aberta pelo apresentador
Aplicando a Teoria de Bayes:
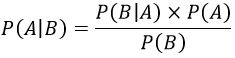
Dessa equação, sabemos que P(A) = ⅓ que foi a primeira probabilidade. Agora precisamos calcular, P(B) e para isso é preciso cobrir todas as probabilidades de o apresentador abrir uma porta vazia.
A equação, ficará então da seguinte maneira:
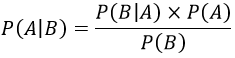
Dessa forma, as probabilidades ficam definidas:
- P(A): Probabilidade de o prêmio estar na porta 1;
- P(B|A): Probabilidade de o apresentador escolher uma porta vazia considerando que o prêmio está na porta 1;
- P(B|A^C): Probabilidade de o apresentador escolher uma porta vazia considerando que o prêmio não está na porta 1;
- P(A^C): Probabilidade de o prêmio não estar na porta 1.
Podemos então dizer que a probabilidade do apresentador escolher uma porta vazia é 1, visto que ele sabe atrás de qual porta está o prêmio. Ou seja, P(B|A) = P(B|A^C) = 1.
Já a probabilidade de o prêmio não estar na porta nº 1 P(A^C) é de ⅔, essa é a chance de errar na primeira escolha. Portanto, se você mantiver a sua escolha, a probabilidade será:
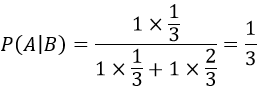
Portanto, se você continuar na sua porta, as suas chances continuam sendo ⅓, mas se você mudar terá mais uma escolha e a probabilidade aumenta para ⅔.
Apesar de não ser intuitivo, a melhor opção no caso é trocar de porta para aumentar as probabilidades de ganho.
Foi possível entender o Teorema de Bayes? Deixe o seu comentário e compartilhe esta matéria com seus amigos nas redes sociais.